Toán học – Những điều kì thú và những mốc son lịch sử (Phần 6)

91. Topo học là gì?

Đó là một phát triển mới trong hình học vào thế kỉ 20 và là một trong những ngành phức tạp và sôi nổi nhất của toán học hiện đại.

Đó là một loại hình học nghiên cứu tính chất của các hình dạng và các mặt vẫn bất biến dưới tác dụng kéo giãn, bẻ cong, co nén, và xoắn.

92. Topo học khác gì với những hình học khác?

Không giống như những hình học khác, topo học không xét độ lớn của các chiều dài và các góc, nó là một môn hình học phi định lượng.

Topo học nghiên cứu các liên hệ chỉ phụ thuộc vào vị trí. Nói cách khác, nó chỉ nghiên cứu tính chất topo học của các hình dạng và các mặt.

93. Tính chất topo học của các hình dạng là gì?

Đây là những tính chất của các hình dạng vẫn không thay đổi ngay cả khi hình dạng đó bị biến dạng nhiều đến mức toàn bộ các tính chất đo lường và xạ ảnh của nó bị mất hết.

Xét một đường tròn (tức chỉ xét riêng đường cong, mà không xét diện tích khép kín bên trong) vẽ trên một tấm cao su. Bằng cách kéo giãn, bóp nén, bẻ cong, xoắn, nhưng không xé, nhập hay chồng, thì nó có thể biến dạng thành một elip, một tam giác, một hình vuông, hay bất cứ hình nào khác đều hay không đều.

Mỗi biến đổi như thế được gọi là một biến đổi topo. Tính chất phân biệt của nó là những bộ phận của hình đang tiếp xúc thì vẫn tiếp xúc, còn những bộ phận không tiếp xúc thì không thể tiếp xúc. Tóm lại, trong một biến đổi topo không thể có sự phân chia hay hợp nhất.

Dưới những tác dụng như thế, các tính chất như khoảng cách, góc, và diện tích bị biến đổi, còn các tính chất topo thì giữ nguyên.

94. Bên trong và bên ngoài! Đây có là những tính chất topo hay không?

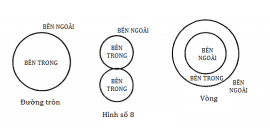
Thực tế đường tròn có một “bên trong” và một “bên ngoài” là một tính chất topo.

Đường hình số 8 có hai vòng và do đó có hai “bên trong” là không tương đương topo với một đường tròn hay một tam giác, vì mỗi hình này chỉ một “bên trong”.

Một cái vòng tạo bởi hai đường tròn đồng tâm thì có hai “bên ngoài” và một “bên trong”.

95. Tính chất topo của các mặt là gì?

Xét bề mặt của một hình cầu. Nó có hai tính chất được bảo toàn dưới một biến đổi topo tùy ý.

Thứ nhất, bề mặt của hình cầu là kín. Kín theo nghĩa là không giống như hình trụ, nó không có cạnh rìa – một hình trụ được liên kết bởi hai cạnh rìa.

Thứ hai, mỗi đường cong kín trên mặt cầu chia mặt cầu thành hai phần tách biệt.

Một cái ống kín hay một cái vòng, gọi là vòng xuyến, thì không có tính chất này. Nếu một vòng xuyến bị cắt vuông góc với chiều dài của nó, thì nó không tách phần hai phần mà bị biến thành một hình ống cong, hình này có thể bị kéo thẳng thành hình trụ bởi phép biến đổi topo. Như vậy, mỗi đường cong kín trên mặt vòng xuyến không tách nó thành hai phần.

Vì thế, mặt cầu và mặt vòng xuyến là những mặt phân biệt về mặt topo học, hay nói theo các nhà topo học là chúng không đồng phôi.

96. Nếu có hai điểm bị lấy ra khỏi mặt cầu thì sao?

Bề mặt của một hình cầu với hai điểm bị loại ra là đồng phôi với một hình cầu có hai chỏm kín bị lấy mất và mỗi hình là đồng phôi với hình trụ. Hình cầu và hình lập phương thuộc cùng loại topo, tức là chúng là đồng phôi.

97. Một cặp găng tay thì sao?

Xét một cặp găng tay. Một cái là găng tay trái và một cái là găng tay phải. Nếu găng tay phải bị lộn từ trong ra ngoài thì nó trở thành găng tay trái. Găng tay trái trở thành găng tay phải nếu nó bị lộn từ trong ra ngoài. Lập luận topo cho phép chúng ta dự đoán sự biến đổi hình dạng này.

98. Những khái niệm căn bản của topo học là gì?

Khái niệm liền kề, lân cận, gần vô hạn và khái niệm tách vật (phân chia thành các bộ phận) là những khái niệm căn bản của topo học.

Một số khái niệm tương tự là bên trong và bên ngoài, bên phải và bên trái, liên kết và mất liên kết, liên tục và không liên tục.

99. Có phải topo học chỉ nghiên cứu các mặt?

Không, nghiên cứu các mặt chỉ là một lĩnh vực thôi. Topo học có nhiều phương diện, nhưng nó thường được chia làm ba phân ngành:

Topo học tổ hợp

Topo học đại số

Topo học tập điểm

Sự phân chia chủ yếu là để tiện lợi chứ không theo logic nào, bởi vì có sự chồng lấn đáng kể giữa các phân ngành topo học.

100. Topo học tổ hợp là gì?

Topo học tổ hợp là nghiên cứu các thuộc tính của những dạng hình học vẫn bất biến dưới các phép biến đổi topo.

Nó xem mỗi hình dạng là một tổ hợp gồm những hình đơn giản nối lại với nhau theo một kiểu liên tục, trái với topo học tập điểm xét các hình dạng là gồm tập hợp của các điểm.

101. Topo học đại số là gì?

Ban đầu, topo học được phát triển là một lĩnh vực nghiên cứu các mặt. Nhưng người ta sớm nhận ra rằng các khái niệm của nó có liên hệ mật thiết với một số bài toán có tầm quan trọng căn bản trong những lĩnh vực đa dạng của toán học. Các phương pháp đại số, nhất là lí thuyết nhóm, tỏ ra hết sức hữu ích trong những nghiên cứu như thế.

Phương pháp đại số này được gọi là topo học đại số và là một công cụ mạnh để chứng minh các kết quả topo học.

Nó cũng mang lại rất nhiều kết quả trong không gian cao chiều, nơi chúng ta không thể nhìn thấy mà chỉ có thể luận giải.

102. Topo học tập điểm là gì?

Trong khi topo học đã và đang được phát triển là một lĩnh vực nghiên cứu các mặt, nhưng người ta cũng nhận ra rằng topo học của riêng các mặt sơ cấp thôi là không đủ và nghiệm của các bài toán trong topo học một, hai, ba và $n$ chiều là cần thiết. Những nghiên cứu này khai thác lí thuyết tập hợp và được phát triển thành topo học tập điểm.

Họ dạng hình học được nghiên cứu trong lĩnh vực topo học này là cực kì rộng rãi. Một điểm trong topo học này có thể biểu diễn một điểm của một hình dạng hình học bình thường, bản thân một hình dạng hoàn chỉnh, hay cả một hệ thống hình học.

103. Vì sao topo học được gọi là hình học tấm cao su?

Một mặt của topo học là nghiên cứu sự biến dạng của những hình dạng mà không xé rách hay nhập các điểm của chúng. Vì những biến dạng như thế có thể được thực hiện trên những hình vẽ trên một tấm cao su, nên topo học thỉnh thoảng được gọi là hình học tấm cao su.

Nhưng topo học hiện đại thì vươn xa ra khỏi phương diện vỡ lòng này.

104. Có phải topo học đương thời là nghiên cứu hình học không?

Lúc mới ra đời, topo học được xem là “khoa học của vị trí”, như tên gọi nghĩa đen của nó, nhưng dần dần nó đã phát triển vượt khỏi tầm vóc ban đầu của nó.

Về sự biến đổi đặc tính của nó, người ta thấy rõ rằng “topo học bắt đầu là nhiều hình học và ít đại số, nhưng bây giờ nó là nhiều đại số và ít hình học”.

Nói theo lịch sử, topo học đã phát triển theo hai hướng rạch ròi. Ở một hướng, cảm hứng dường như đến từ hình học, còn ở hướng kia giải tích có tầm ảnh hưởng chính.

105. Có đúng không nếu nói topo học là nghiên cứu tính liên tục?

Ngày nay, người ta thường chấp nhận rằng topo học là nghiên cứu tính liên tục.

Nhưng quan trọng hơn hết thảy, nó đã trở thành một ngành học nỗ lực hợp nhất hầu như toàn bộ toán học có chút tương tự với tìm kiếm triết học để sáp nhập toàn bộ kiến thức.

Ngày nay, topo học xâm nhập sâu vào toán học đến mức nó là một công cụ không thể thiếu của nhà toán học hiện đại, dù là toán lí thuyết hay toán ứng dụng.

106. Nói topo học là toán học của cái khả dĩ là có nghĩa như thế nào?

Đây là vì có nhiều câu hỏi chưa được trả lời trong những ngành toán học khác nhưng đã được xác định rõ ràng bằng cách áp dụng các khái niệm topo học.

Ví dụ, topo học xét những bài toán nhất định nào thì nghiệm có tồn tại hoặc không tồn tại, mặc dù nó thường không cho biết làm thế nào tìm ra nghiệm.

Tương tự, nó có thể cho biết những điều kiện nhất định nào là có thể hay không thể.

107. Có ví dụ nào đặc biệt không?

Xét một trường hợp từ đại số. Cái gọi là “định lí cơ bản của đại số” phát biểu rằng

Mỗi phương trình đại số bậc $n$ bất kì với các hệ số thực hay phức

$$x_{n} + a_{1}x^{n-1} + a_{2}x^{n-2} +... + a_{n} = 0$$

đều có nghiệm trong trường số phức.

Đây là một tình huống đại số thuần túy, tức là một phương trình dù có nghiệm hay không, nhưng không có chứng minh đại số thuần túy nào của kết quả quan trọng này. Mọi chứng minh đòi hỏi kiến thức giải tích hàm của vài biến số thực, hay giải tích phức.

Nhưng kể từ khi các khái niệm và các phương pháp topo học làm biến đổi phần lớn những ngành toán học này hầu như vượt ra ngoài thừa nhận, người ta thường tin rằng định lí trên về cơ bản phụ thuộc vào các xét đoán topo học.

108. Có ví dụ nào khác nữa không?

Một lần nữa, xét một trường hợp từ các phương trình vi phân. Đa số các hiện tượng vật lí và các bài toán của công nghệ hiện đại có thể được mô tả toán học bởi những phương trình vi phân, tức là những phương trình chứa các tốc độ biến thiên. Trong những nghiên cứu này, các phương trình vi phân phi tuyến xuất hiện thường xuyên nhưng chúng cực kì khó giải. Topo học có thể chỉ ra những loại nghiệm nào của những phương trình vi phân phi tuyến nhất định là có thể, mặc dù ở đây một lần nữa đáp số là định tính chứ không định lượng.

Trong ngữ cảnh như thế thì topo học được mô tả là toán học của cái có thể.

109. Các khái niệm topo có bất kì ứng dụng thực tế nào không?

Các khái niệm topo được sử dụng trong thiết kế các mạng lưới, nghĩa là trong phân phối điện, khí đốt và nước, và trong thiết kế tự động công nghiệp.

Chúng được sử dụng trong điều khiển lưu lượng giao thông và dẫn hướng tên lửa.

Chúng còn được áp dụng trong thiết kế bản đồ địa lí.

Lí thuyết các hệ thống động lực phong phú là nhờ các khái niệm và ý tưởng topo học.

Lí thuyết hàm hiện đại và logic biểu tượng có liên hệ mật thiết với topo học.

110. Mặt một bề là gì?

Lấy một băng giấy và dán hai đầu lại với nhau, $A$ trùng với $C$, và $B$ với $D$. Cách này cho ta một mặt trụ.

Mặt trụ có hai mặt – mặt trong và mặt ngoài – một mặt, ví dụ, có thể sơn màu xanh, còn mặt kia sơn màu đỏ.

Đồng thời, nó có hai cạnh, cạnh trên và cạnh dưới. Bây giờ lấy một băng giấy khác, xoắn nó nửa vòng rồi dán lại lần này sao cho $A$ trùng với $D,$ và $B$ với $C$. Đây là dải Mobius nổi tiếng, do nhà toán học người Đức A. F. Mobius khám phá vào năm $1858$.

Nếu chúng ta cố sơn hai mặt của vật này bằng hai màu, ta sẽ thấy rằng không thể làm được, vì nó chỉ có một mặt!

Trông có vẻ lạ, nhưng đáng để bạn làm thử với một băng giấy hay một dải lụa.

111. Tinh thần của thí nghiệm này là gì?

Nó cho thấy ngay cả điều quả quyết rõ ràng đơn giản và chân thật rằng mỗi bề mặt có hai mặt có thể là sai lầm! Do đó, trong toán học, chứng minh logic chặt chẽ là cần thiết, cho dù điều khẳng định có hiển nhiên như thế nào.

112. Dải Mobius có tính chất nào khác hay không?

Một tính chất nổi bật nữa của mặt này là có chỉ có một cạnh, một đường khép kín! Nếu dây curoa được xoắn lại nửa vòng trước khi thắt thì nó trở thành một mô hình của dải Mobius. Một dây curoa như vậy có thể tồn tại lâu hơn vì nó bị mòn đều ở hai mặt do ma sát trên bánh xe. Thật vậy, nó chỉ có một mặt và một cạnh.

Một lần nữa, nếu chúng ta cắt mặt trụ theo phương vuông góc với trục của nó dọc theo đường giữa, thì ta được hai mặt trụ. Nhưng nếu chúng ta cắt dải Mobius theo đường giữa, thì nó vẫn là một dải! Bạn hãy lấy một băng giấy để xác nhận. Sẽ thú vị đấy.

113. Công thức Euler cho hình khối là gì?

Công thức nêu một liên hệ giữa các đỉnh, các cạnh và các mặt của một hình khối đơn giản.

Nó phát biểu rằng đối với một khối đa diện đơn giản bất kì thì

$$V – E + F = 2$$

trong đó $V$ là số đỉnh, $E$ là số cạnh, và $F$ là số mặt.

Để minh họa, một hình hộp chữ nhật hoặc hình lập phương thì có $8$ đỉnh, $12$ cạnh và $6$ mặt, nên $8 – 12 + 6 = 2$, thỏa mãn công thức.

Tương tự, một tứ diện có $4$ đỉnh, $6$ cạnh và $4$ mặt, nên $4 – 6 + 4 = 2$, một lần nữa thỏa mãn công thức.

114. Nhưng làm thế nào công thức này là kết quả trong topo học?

Công thức trên vẫn đúng khi hình khối chịu mọi kiểu biến dạng topo, trong khi, nói chung, các cạnh thôi không còn thẳng, và các mặt thôi không còn phẳng và biến thành những mặt cong.

Vì thế, công thức này được người ta cho là định lí đầu tiên về mặt lịch sử trong topo học.

Nó đã được Descartes biết tới vào khoảng năm $1640$, nhưng được khám phá lại bởi Euler vào năm $1752$.

115. Bài toán Bảy chiếc cầu Koenigsberg là gì?

Thành phố Koenigsberg có trung tâm nằm trên một cù lao trên sông Pregel. Vào thế kỉ $17$, cù lao này được nối với hai bờ sông với hai chiếc cầu ở mỗi bờ. Cù lao này còn có một chiếc cầu bắt sang một cù lao lân cận, và cù lao kia được nối với mỗi bờ sông bằng một chiếc cầu.

Sơ đồ như sau:

Câu đố khó dành cho các công dân của thành phố như sau:

Làm thế nào vạch ra hành trình đi qua tất cả bảy cây cầu mà không được đi qua bất kì cây cầu nào hai lần?

Đây chính là bài toán Bảy chiếc cầu Koenigsberg.

116. Làm thế nào có thể lập ra một hành trình như thế?

Một hành trình như thế không thể nào vạch ra được. Các thử nghiệm lặp đi lặp lại cho thấy không thể làm được chuyện đó, nhưng Euler đã đưa ra nguyên tắc chung cho những bài toán như vậy gọi là các bài toán mạng trong topo học.

117. Nguyên tắc đó là gì?

Trước khi có thể giải thích nguyên tắc, chúng ta nên nhớ trong đầu một vài khái niệm và thuật ngữ.

Để cho đơn giản, các vùng đất được thay bằng các điểm, và các cây cầu bắt qua sông được thay bằng các đoạn nối giữa các điểm.

Các điểm đó được gọi là đỉnh. Một đỉnh là lẻ hoặc chẵn, theo số lượng đường dẫn từ đỉnh đó là lẻ hay chẵn.

Euler đã khám phá rằng:

(i) Nếu tất cả các đỉnh trong một mạng liên kết đều là chẵn thì mạng đó có thể được đi xuyên trong một hành trình bắt đầu và kết thúc tại cùng một đỉnh như trong các trường hợp sau:

(ii) Nếu mạng chứa hai đỉnh lẻ, thì nó có thể được đi xuyên trong một hành trình, nhưng không thể quay về tại điểm xuất phát.

(iii) Nếu mạng chứa $4, 6$ hoặc $8$ đỉnh lẻ, thì tương ứng sẽ cần $2, 3$ hoặc $4$ hành trình riêng để đi qua nó. Số lượng hành trình cần thiết để đi xuyên một mạng liên kết bằng nửa số đỉnh lẻ.

(iv) Một mạng gồm một số lẻ đỉnh lẻ thì không thể dựng được bởi vì mỗi đường cần bắt đầu tại một đỉnh và kết thúc tại một đỉnh.

118. Nguyên tắc trên được áp dụng như thế nào cho bài toán Bảy chiếc cầu Koenigsberg?

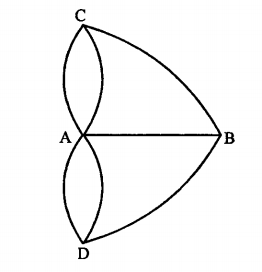
Trong bài toán đó, khi hai cù lao được thay bằng hai điểm $A$ và $B$, con sông chia tách hai phần đất được kí hiệu là $C$ và $D$, và bảy chiếc cầu được kí hiệu bằng bảy đường cung, mạng đã cho có dạng như sau:

Vì trong trường hợp này, cả bốn đỉnh đều là lẻ, nên cần có hai hành trình mới đi hết mạng lưới. Một hành trình duy nhất là không thể.

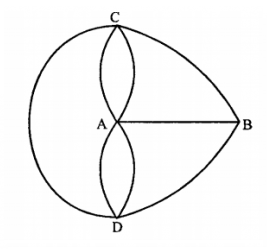
119. Nếu có thêm một cầu nữa bắt qua sông thì sao?

Nếu xây thêm một chiếc cầu nữa bắt qua sông, trên sơ đồ được vẽ bằng nét đứt ở phía cùng bên trái, thì mạng có dạng như sau:

Trong trường hợp này, hai đỉnh $C$ và $D$ đều chẵn, và hai đỉnh kia, $A$ và $B$, đều là lẻ. Bây giờ một hành trình là đủ, nhưng hành trình đó phải bắt đầu tại một đỉnh lẻ, $A$ hoặc $B$, và kết thúc tại đỉnh kia.

120. Tại sao bài toán trên lại được đánh giá quan trọng thế?

Bởi vì cùng với đáp số của bài toán đã ra đời một ngành toán học hoàn toàn mới.

Khi Euler giới thiệu lời giải trước Viện hàn lâm nước Nga ở St Petersburg vào năm $1736$, không những một bài toán dai dẳng đã được giải mà cùng với nó Topo học đã ra đời.

121. Hình ngôi sao và hình chữ nhật với hai đường chéo thì có đi xuyên qua một lượt được không?

Hình ngôi sao có 10 đỉnh, mỗi đỉnh đều chẵn. Do đó, chẳng khó khăn gì để vẽ nó bằng một nét duy nhất.

Hình chữ nhất với hai đường chéo có 5 đỉnh, gồm bốn đỉnh lẻ và một đỉnh chẵn. Do đó, cần có hai hành trình. Nó không thể được vẽ bằng một nét.

(còn tiếp)