Toán học – Những điều kì thú và những mốc son lịch sử (Phần 5)

73. Hình học giải tích là gì?

Lĩnh vực nghiên cứu các đường cong và các mặt với sự hỗ trợ của toán học giải tích được gọi là hình học giải tích.

Hình học giải tích nghiên cứu những bài toán đa dạng vượt ra ngoài phép tính độ dốc và độ cong.

Nó cũng nghiên cứu bài toán rất quan trọng của trắc đạc, tức là bài toán xác định khoảng cách ngắn nhất giữa hai điểm trên một bề mặt.

74. Hệ tọa độ ba chiều là gì?

Nếu ta bổ sung thêm một trục $Oz$ vuông góc với trục $Ox$ và $Oy$, tức là vuông góc với mặt phẳng trang giấy và đo các khoảng cách song song với $Ox, Oy$ và $Oz$ theo trật tự đó, thì một điểm $P$ trong không gian có thể được xác định bởi bộ ba số thực xếp theo trật tự $(x_{1}, y_{1}, z_{1})$.

Ngược lại, một bộ ba số thực bất kì xếp theo trật tự xác định duy nhất một điểm trong không gian. $(x_{1}, y_{1}, z_{1})$ được gọi là các tọa độ của điểm $P$.

Hình học tọa độ ba chiều nghiên cứu các điểm trong không gian hay, tương đương, những bộ ba số trật tự.

75. Hình học $n$ chiều là gì?

Cayley và nhà toán học người Đức Grassmann, độc lập nhau, đã khái quát hóa hình học tọa độ hai chiều.

Trong hình học tọa độ hai chiều, một điểm được xác định bởi hai tọa độ và khoảng cách giữa hai điểm có tọa độ $(x_{1}, y_{1})$ và $(x_{2}, y_{2})$ được cho bởi

Theo định lí Pythagoras:

$$PQ^{2}=PM^{2}+MQ^{2}$$

Hay:

$$PQ^{2}=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$$

$$\Rightarrow PQ=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$

Tương tự, trong hình tọa độ ba chiều, khoảng cách giữa 2 điểm của tọa độ $(x_{1};y_{1};z_{1})$ và $(x_{2};y_{2};z_{2})$ được cho bởi:

$$\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}$$

Biểu thức này có thể được khái quát hóa, và trong hình học tọa độ bốn chiều, khoảng giữa hai điểm có tọa độ $(x_{1}, y_{1}, z_{1}, t_{1})$ và $(x_{2}, y_{2}, z_{2}, t_{2})$ được cho bởi:

$$\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})+(t_{2}-t_{1})^{2}}$$

Ta có thể tiếp tục khái quát hóa cho hình học tọa độ n chiều, khoảng giữa hai điểm có tọa độ $(x_{1}, x_{2}, x_{3}, x_{4},..., x_{n})$ và $(y_{1}, y_{2}, y_{3}, y_{4},..., y_{n})$ được cho bởi:

$$\sqrt{(y_{1}-x_{1})^{2}+(y_{2}-x_{2})^{2}+(y_{3}-x_{3})^{2}+(y_{4}-x_{4})^{2}+...+(y_{n}-x_{n})^{2}}$$

Mỗi khái niệm trong hình học hai chiều có thể khái quát hóa thành một khái niệm tương đương n chiều. Vì không gian mà chúng ta đang sống trong đó là ba chiều, nên trực quan hình học không thể cảm nhận vượt quá ba chiều, nhưng sự tương tự là rất có ích.

76. Hình học tọa độ bốn chiều có ứng dụng gì?

Hình học tọa độ bốn chiều có công dụng lớn đối với các nhà vật lí.

Giống hệt như một điểm trong một mặt phẳng hoàn toàn được xác định bởi hai con số gọi là tọa độ và một điểm trong không gian được xác định bởi ba tọa độ, một sự kiện được xác định bởi ba tọa độ cho biết vị trí trong không gian và tọa độ thứ tư cho biết thời điểm xảy ra.

Khoảng cách giữa hai sự kiện, tức là khoảng cách không-thời gian, như nó thường được gọi, được cho bởi

$$\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})+(t_{2}-t_{1})^{2}}$$

Hình học này đã được khai thác làm một công cụ thiết yếu trong phát triển của thuyết tương đối và trong nghiên cứu không gian, thời gian và lực hấp dẫn.

77. Khái niệm không gian trong toán học là gì?

Thuật ngữ không gian có hai ý nghĩa.

Hiểu theo một nghĩa nó là không gian thật sự bình thường, tức là không gian trải nghiệm của chúng ta.

Hiểu theo nghĩa khác, thì nó là “không gian trừu tượng”, tức là xét một tập hợp những đối tượng đồng nhất trong đó các liên hệ dạng không gian là đúng. Ví dụ, “khoảng cách” giữa hai vật có thể được xác định trong không gian này.

Trong toán học, người ta thường hiểu theo hàm nghĩa thứ hai.

78. Điểm là gì?

Khái niệm điểm trong hình học tọa độ hai chiều là nguyên tố không gian có vị trí có thể được cố định bởi hai khoảng cách. Do đó, không gian hai chiều có thể được xem là một tập hợp gồm tất cả những nguyên tố đó có vị trí có thể được cố định bởi hai chiều dài.

Tương tự, không gian ba chiều có thể được xem là một tập hợp gồm tất cả những nguyên tố có vị trí có thể được cố định bởi ba chiều dài.

Với ba tọa độ là đã đạt tới giới hạn của nhận thức trực quan vì người ta không thể nào hình dung ra trong không gian thật vị trí của một điểm với bốn hoặc nhiều tọa độ.

79. Làm sao nhận thức được không gian $n$ chiều?

Thay vì gán ba chiều dài để cố định vị trí của một điểm trong không gian ba chiều, ta hãy nói rằng ta gán ba con số để cố định điểm đó. Khi này, điểm đó là một bộ ba trật tự đơn thuần và không cần thiết xem nó nằm trong một không gian thật sự nơi mắt chúng ta có thể nhìn vào.

Một khi dẹp bỏ được cái bản năng hình dung thị giác phiền toái kia và một điểm được nhận định là một bộ ba con số, thì ta chẳng có gì ngần ngại để thay con số $3$ bằng số tổng quát $n$. Và chúng ta có một “không gian” $n$ chiều, trong đó $n$ có thể nhận giá trị lớn hơn $3$.

Khi đó, một “điểm” tốt hơn nên được gọi là một “nguyên tố” và “không gian” là “đa diện”.

80. Đa diện có là một khái niệm tổng quát hơn không?

Tên gọi “đa diện” mang tính khái quát hơn và chính xác hơn thuật ngữ “không gian”.

Một đa diện đại khái giống như một lớp.

Một mặt phẳng là một lớp gồm tất cả những điểm được xác định duy nhất bởi hai tọa độ, và do đó nó là một đa diện hai chiều.

Tương tự, không gian của hình học tọa độ ba chiều có thể được xem là đa diện ba chiều vì ba tọa độ là cần thiết để cố định những điểm nằm trong đó.

Nếu cần $n$ con số hay tọa độ để cố định mỗi nguyên tố của một đa diện, dù nó là không gian hay một lớp bất kì nào khác, thì nó được gọi là một đa diện $n$ chiều.

Đa diện được cho là không có thuộc tính, ngoại trừ việc nó là một lớp.

81. Chúng ta có những đa diện khác nữa không?

Chúng ta có nhiều loại đa diện chẳng có liên quan gì đến không gian hay hình học. Một đa diện ba chiều sẽ là một lớp nguyên tố, mỗi nguyên tố trong đó sẽ cần đúng ba con số để xác định nó.

Một nhóm người có thể được xem là một đa diện – và một đa diện ba chiều, với ba con số $x_{1}, x_{2}, x_{3}$ biểu diễn tuổi tác, chiều cao và cân nặng, là cần và đủ để phân biệt họ.

Cũng nhóm người đó có thể được xem là một đa diện bốn chiều, nếu bốn con số $x_{1}, x_{2}, x_{3}, x_{4}$ biểu diễn tuổi tác, chiều cao, cân nặng, và số nhà được sử dụng. Nhóm người đó trở thành một đa diện năm chiều nếu bổ sung thêm một con số $x_{5}$ biểu diễn thu nhập.

Chúng ta cũng có thể nghĩ tới một đa diện bốn chiều gồm các hạt chất khí, sử dụng ba chiều để cố định vị trí của chúng và một chiều cố định mật độ của chúng.

82. Ưu điểm của biểu diễn như thế là gì?

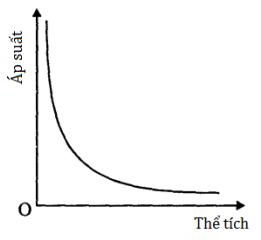
Giả sử chúng ta muốn minh họa sự phụ thuộc của áp suất chất khí vào thể tích của nó.

Ta làm việc này bằng cách dựng hai trục trong một mặt phẳng, dùng một trục biểu diễn thể tích, còn trục kia là áp suất. Đường cong thu được sẽ là một hyperbol cho một chất khí lí tưởng ở nhiệt độ không đổi.

Nếu chúng ta có một hệ phức tạp hơn có trạng thái được cho không phải bởi hai thuộc tính mà nói ví dụ năm thuộc tính, thì đồ thị biểu diễn hành trạng của nó liên quan đến một không gian năm chiều, tức là trạng thái của hệ này có thể được xem là một điểm trong một không gian năm chiều nào đó.

Tương tự, nếu trạng thái của một hệ được cho bởi n thuộc tính, hay n biến, thì trạng thái của nó có thể được xem là một điểm trong một không gian n chiều nào đó.

Ưu điểm của cách biểu diễn như thế là việc nghiên cứu một hệ được thực hiện bằng cách áp dụng và mở rộng các tương đương hình học và các khái niệm quen thuộc.

83. Có phải không gian thực tế của chúng ta nằm trong một không gian bốn chiều?

Khái niệm chiều thứ tư chỉ là một khái niệm trừu tượng được sáng tạo ra để mô tả theo ngôn ngữ hình học những ý tưởng không thể mô tả được bằng những biểu diễn hình học bình thường.

Nó được phát triển để đáp ứng yêu cầu của các hệ phụ thuộc vào vài ba biến số. Nhưng nó được dự tính chỉ là một phương pháp toán học mô hình hóa các hiện tượng vật lí và không liên quan gì với bản chất của không gian thực tế, chỉ có trong tiểu thuyết khoa học mới thường mô tả chiều không gian thứ tư.

Quan điểm cho rằng không gian ba chiều của chúng ta dìm trong một không gian bốn chiều thực sự là chất liệu của tư duy thần bí và chỉ là một sự xuyên tạc của những khái niệm khoa học.

84. Có thể áp dụng các khái niệm hình học cho đại số hay không?

Những bài toán đại số liên quan đến hai hay ba biến thường có cách hiểu hình học. Điều này có nghĩa là nếu một bài toán có một nghiệm đơn giản hoặc rõ ràng từ góc độ hình học, thì nghiệm đó cũng có ý nghĩa cho bài toán xét về phương diện đại số.

Một ví dụ sẽ làm sáng tỏ vấn đề.

Giả sử chúng ta muốn biết những nghiệm nguyên của bất đẳng thức

$$x^{2}+y^{2}<N$$

Về mặt hình học, bất đẳng thức $x^{2} + y^{2} < N$ biểu diễn phần bên trong của vòng tròn có tâm tại gốc tọa độ và bán kính bằng $\sqrt{N}$ , và bài toán được đơn giản thành như sau:

Có bao nhiêu điểm với tọa độ nguyên nằm bên trong vòng tròn bán kính $\sqrt{N}$?

Những điểm như thế là đỉnh của những hình vuông có cạnh bằng đơn vị chiều dài bên trong hình tròn. Số lượng điểm như thế nằm bên trong vòng tròn xấp xỉ bằng số lượng hình vuông nằm bên trong hình tròn, bằng diện tích của hình tròn bán kính .

Do đó, số lượng nghiệm nguyên của bất đẳng thức trên là khoảng $\pi N$.

Sai số ở kết quả tiến về không đối với những giá trị lớn của $N$.

Rõ ràng đáp số mặc dù hiển nhiên về mặt hình học nhưng không hiển nhiên từ phương diện đại số.

85. Kết quả trên có cái tương đương trong không gian cao chiều hơn hay không?

Bài toán tương ứng theo ba biến có thể được giải tương tự, nhưng nếu số lượng biến tăng vượt quá ba, thì phương pháp trên không còn áp dụng được.

Tuy nhiên, kết quả trên có thể được khái quát hóa cho bất kì số lượng biến nào để bài toán tương ứng theo n biến có một nghiệm trong đại số, mặc dù cách hiểu hình học không còn khả dụng vì không gian thực của chúng ta chỉ có ba chiều.

86. Hình học của không gian màu là gì?

Không gian được xem là một tập hợp của các điểm. Nhưng nếu các “điểm” là các vật, các sự kiện hay các trạng thái, thì tập hợp này có thể được xem là một “không gian” thuộc loại riêng của nó.

Khi đó, các khái niệm điểm, đường thẳng, khoảng cách,... được sử dụng với một ý nghĩa đã biến cải nhiều.

Một ví dụ của không gian như thế là không gian màu.

87. Không gian này tương ứng với hình học như thế nào?

Thị giác bình thường của con người có căn nguyên là ba màu. Sự cảm nhận một màu $C$ là kết hợp của ba cảm nhận cơ bản: đỏ $R$, lục $G$ và lam $B$ với cường độ khác nhau, cho nên ta có

$$C = xR + yG + zB$$

trong đó $x, y, z$ là kí hiệu cường độ, tính theo những đơn vị nhất định.

Một điểm có thể di chuyển trong không gian sang trái sang phải, ra trước ra sau, lên trên xuống dưới, cho nên sự cảm nhận màu sắc có thể biến thiên liên tục theo ba chiều bằng cách thay đổi các thành phần $R, G$ và $B$ của nó.

Tập hợp gồm tất cả những màu có thể có, do đó, được xem là không gian màu ba chiều.

Vì các cường độ không thể âm, nên $x, y$ và $z$ luôn luôn dương. Khi $x = 0, y = 0, z = 0$, ta không có màu gì hết (màu sắc vắng mặt hoàn toàn).

88. Điểm, đoạn và khoảng cách được định nghĩa như thế nào trong không gian này?

Ở đây, một “điểm” là một màu, “đoạn” $AB$ là tập hợp thu được bằng cách trộn các màu $A$ và $B$. “Khoảng cách” giữa hai màu được định nghĩa là độ dài của đường ngắn nhất nối giữa chúng. Phép đo chiều dài và khoảng cách trong không gian màu, do đó, được định nghĩa bởi một hình học phi Euclid nhất định.

89. Hình học của không gian màu có ứng dụng gì hay không?

Hình học của không gian màu cung cấp một cơ sở toán học chính xác để giải những bài toán về chất nhuộm trong ngành công nghiệp dệt, giúp phân biệt các tín hiệu màu, và những lĩnh vực có liên quan.

90. Hình học hữu hạn là gì?

Khái niệm không gian của chúng tôi là một tập hợp gồm các điểm hay các nguyên tố, chúng có số lượng vô hạn. Nhưng chúng ta còn có hình học của chỉ một số hữu hạn các điểm, ví dụ như $25$ chẳng hạn.

Các tên gọi điểm, đường thẳng, khoảng cách, song song,... được sử dụng với ý nghĩa thích hợp cho hệ đang nghiên cứu.

Một hình học hữu hạn như thế áp dụng cho những bài toán nhất định, và đại số và lí thuyết số; và nó còn có ích trong lí thuyết mật mã và trong xây dựng các thiết kế thực nghiệm.

(còn tiếp)